- Feature Selection
- Dimension Reduction
- Clustering
- Classification
- Hyperparameter Tuning
- Gene Contributions
- Strategies to Address Data Imbalance
- References
Feature Selection
Working with genetic data presents a challenge due to its high dimensionality, with tens of thousands of genes and only hundreds of samples from patients. Using such data directly to train ML algorithms is likely to generate an overfitted model. Dimensionality reduction is a critical step in preprocessing high-dimensional data to reduce the number of input variables and hence improve the effectiveness of downstream modeling. This process can be particularly beneficial in contexts with many features, where not all features contribute significantly to the predictive model.
To address this challenge, we adopted a two-step approach for dimensionality reduction:
- Feature selection: This step involves selecting a subset of the most important features.
- Dimension reduction: This step involves transforming input features into a lower-dimensional space by identifying patterns and correlations among features.
By using this combination of feature selection and dimension reduction methods, we effectively reduced the high-dimensional input to a very small number of predictors that retain the most relevant information. This reduction is crucial for building robust, non-overfitting classifiers.
We describe our methods for feature selection in the follwoing sections. We explored two commonly used methods for feature selection in machine learning: variance thresholding and univariate selection, and one method commonly used in bioinformatics literature, differential gene expresssion analysis.
Variance Thresholding
Variance thresholding is a simple approach to screen out uninformative features. It removes all features with variance below a certain threshold, under the assumption that features with low variance do not contribute much information. For instance, a feature with constant values (zero variance) adds no predictive value, as it remains unchanged across observations.
We applied a variance threshold of 0.2 to exclude features with low variance. This step removed 986 out of 17126 genes.
Univariate Selection
Univariate feature selection examines each feature’s relationship with the response variable independently. This method uses univariate statistical tests like ANOVA or mutual information measures to select features based on their individual strength of association with the target variable. Univariate selection is straightforward and can be very effective, but it may overlook interactions between features since it evaluates them in isolation.
We employed two univariate feature selection methods, each with its own advantages:
- F-test statistic: test for statistical significance of linear relationships between the indepdendent and dependent variables;
- Mutual information: measures the dependence (including non-linear relationships) between two random variables
Univariate feature selection methods were applied to each gene with respect to the healthy vs cancer label. The distribution of feature relevance scores for both methods is shown in Figure 1. The top 200 genes from each univariate feature selection method were considered.
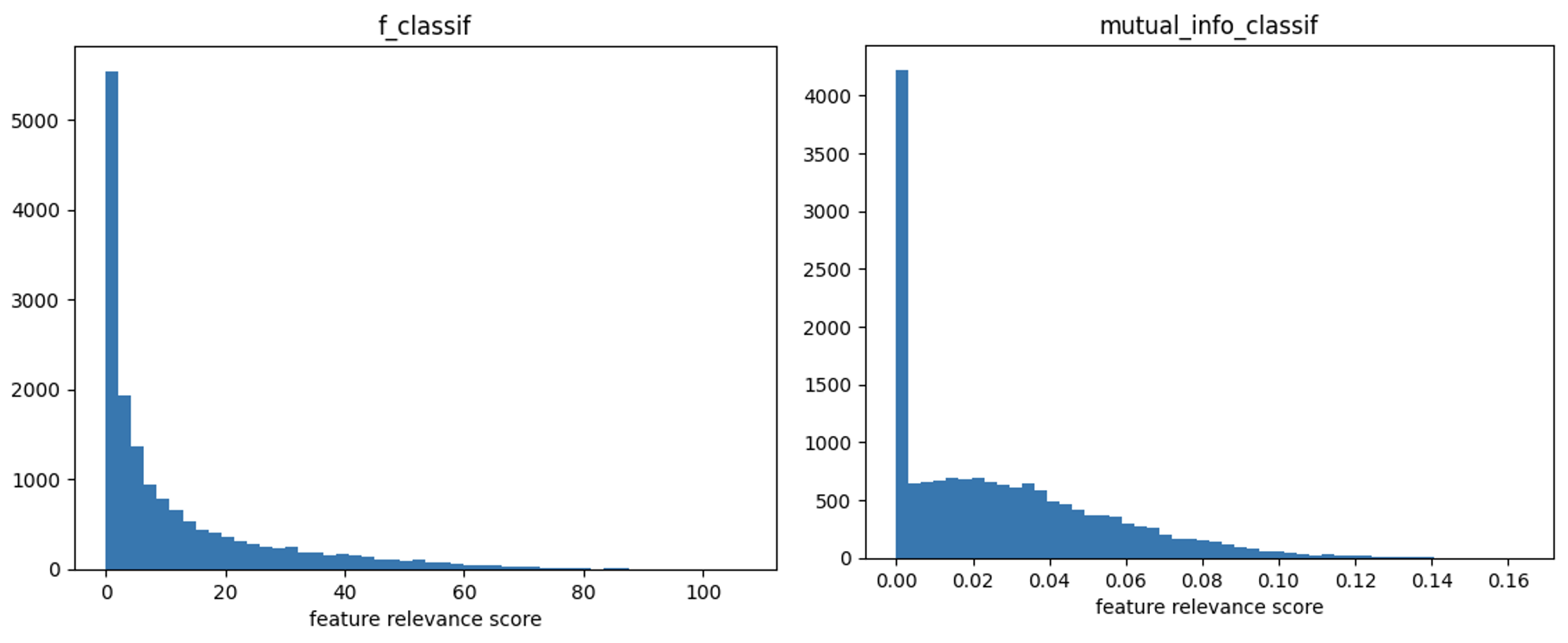
Figure 1: Distribution of feature relevance score of F-test (left) and mutual-information (right) across genes.
The final set of selected features comprises the union of features selected through both criteria, resulting in 312 genes.
Differential Gene Expression
One limitation of using univariate feature selection is that the same set of features are used for cancer status classification as well as classificaiton of different cancer types. In reality, different cancers are caused by different biological and molecular mechanisms, and the use of the same features to detect different cancers may lead to poor accuracy and recall.
Differential gene expression is an analysis that is frequently conducted to understand transcriptional differences between samples of different conditions. We used PyDESeqq2 [1] to determine the top differentially expressed genes for each of our binary tests (healthy versus cancer, colon cancer versus non-colon cancer, etc). PyDESeq2 requires RNA count data as input. Given that the GSE81314 dataset was in RPKM, we were limited to using GSE89570 data for DGE. To avoid contaminating our testing data with label information, we only included GSE98570 samples present in the training data for DGE calculations. We determined the top differentially expressed genes based on adjusted p-values, to account for inflated chances of identifying spurious “significant” genes originating from multiple comparisons. To determine the most informative number of genes, we used the elbow method with plots of adjusted p-values ordered by ascending value.

Figure 2: Graphs of differentially expressed gene adjusted p-values ordered by ascending adjusted p-value.
Dimension Reduction
After feature selection, further dimension reduction is necessary due to the small sample size of our data. We expect that some features are highly correlated since genes are functionally related. Latent variable methods can consider such correlations in high-dimensional datasets and extract compact, non-overlapping representations of original features.
We tried three dimension reduction methods: Principal Component Analysis (PCA), Uniform Manifold Approximation and Projection (UMAP), and Partial Least Squares (PLS).
Principal Component Analysis (PCA)
PCA is a linear technique used to reduce the dimensionality of a dataset while retaining as much variability as possible. It works by identifying the directions, or principal components, that maximize the variance in the data. These components are orthogonal to each other and provide a new basis for representing the dataset. PCA is best suited for datasets where linear relationships are dominant, and it’s often used for noise reduction, visualization, and feature extraction.
The key steps in PCA include:
- Standardization: Often, the data is standardized to have a mean of 0 and a variance of 1.
- Covariance Matrix Computation: Calculate the covariance matrix to understand how variables relate to one another.
- Eigenvalue and Eigenvector Calculation: From the covariance matrix, compute the eigenvalues and their corresponding eigenvectors. These eigenvectors are the principal components.
- Projection: Project the original data onto the space spanned by the principal components selected based on their eigenvalues.
Uniform Manifold Approximation and Projection (UMAP)
UMAP reduces dimensionality by preserving the local and, to some extent, global structure of the data. Unlike PCA, UMAP is capable of uncovering non-linear structures within the data, particulary important in the field of genomics where the intrinsic data structure is non-linear. It works on the principle of manifold learning and topological data analysis. The process involves:
- Construction of a High-Dimensional Graph: Create a weighted graph representing the data in the original high-dimensional space, focusing on preserving the local neighborhood of each point.
- Optimization of a Low-Dimensional Graph: Construct a similar graph in the lower-dimensional space and iteratively adjust it to make the low-dimensional graph’s structure as similar as possible to the high-dimensional graph structure, using a cost function to compare the two graphs.
Supervised UMAP extends the unsupervised UMAP algorithm by incorporating label information into the embedding process. It does this by optimizing the layout of the data points not only based on their similarity but also ensuring that points with the same label are closer together, enhancing the class separability in the reduced dimension space.
Partial Least Squares
Based on the high accuracy and recall of the training data versus the poorer performance on the testing data observed with our supervised UMAP embeddings, we decided to adopt a dimension reduction approach less prone to overfitting. PLS uses labels indirectly, aiming to maximize the correlation between features and labels, thereby potentially enhancing the generalizability of our model while still leveraging label information. The PLS components were then used as input for our classification models.
Discussion
There are several differences between these methods:
- Linearity: PCA and PLS are linear algorithms, meaning they are best at capturing the global structure and linear relationships within the data. UMAP, on the other hand, is non-linear and excels at preserving both local and global structures, even in complex datasets.
- Interpretability: The components derived from PCA and PLS have a direct linear interpretation in terms of the original features. UMAP provides a more abstract representation that, while excellent for clustering and visualization, may offer less straightforward interpretability.
- Flexibility: UMAP offers more flexibility through its parameters (such as the number of neighbors) to balance between local and global data structure preservation. PCA mainly focuses on global variance. PLS focuses on maximizing correlations.
- Computational Complexity: PCA and PLS can be more computationally efficient, especially for very large datasets, due to well-optimized linear algebra routines. UMAP’s computational complexity is higher, but it provides significant advantages in revealing complex patterns.
- Supervision: While PCA is a purely unsupervised dimension reduction algorithm that focuses on maximizing variance, UMAP and PLS have capability to use labels to do supervised dimension reduction.
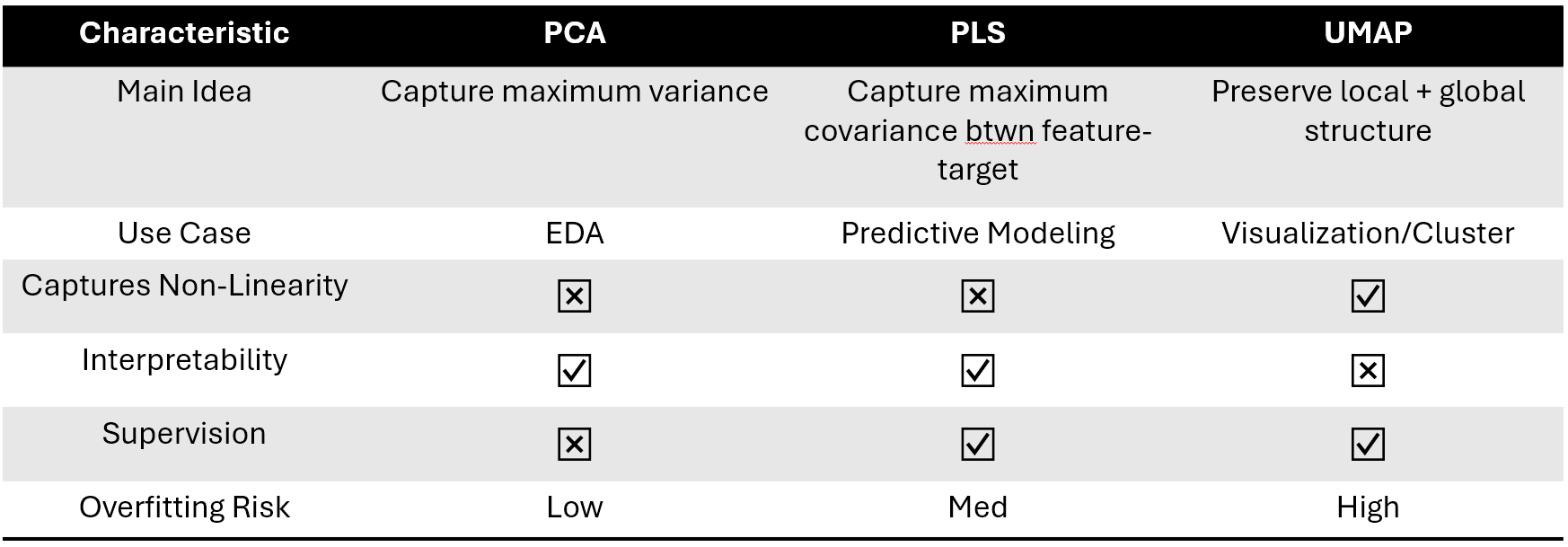
Figure 3: Characteristics of dimension reduction methods.
Clustering
To better understand what patterns exists in cell-free DNA data, we applied clustering as part of Exploratory Data Analysis (EDA) before building classification models. We compared four popular clustering algorithms: K-Means, DBSCAN, hierarchical clustering, and Gaussian Mixture Models.
Models
- K-means algorithm works by iteratively assigning each data point to the nearest cluster centroid and then recalculating the centroid of each cluster based on the assigned points. K-means is computationally efficient and can handle large datasets with ease. While it assumes spherical clusters, it performs well even when this assumption is not met as is the case here. We ran K-Means multiple times to ensure it does not get stuck in a local minimum.
- Hierarchical clustering is an agglomerative clustering method that begins by treating each data point as a single cluster and then iteratively merges the closest pairs of clusters until the desired number of clusters is reached. These hierarchical clustering results can be valuable for downstream analysis, as they illustrate how clusters are related to each other and will help us identify hard-to-distinguish cancer types.
- DBSCAN. Unlike traditional clustering algorithms, DBSCAN (Density-Based Spatial Clustering of Applications with Noise) does not require the user to specify the number of clusters in advance. Instead, it implicitly determines the number of clusters based on the density of datapoints and in doing so, can categorize outliers as noise. This is especially important given the noisy nature of our dataset. Furthermore, DBSCAN is capable of handling clusters of varying shapes, sizes and densities which is also important for our data as evident in our UMAP embeddings.
- Gaussian Mixture Models (GMMs) are probabilistic models that assume the data is generated from a mixture of several Gaussian distributions, each with its own mean and covariance. Unlike K-means, which assumes spherical clusters, GMMs are more flexible and can capture complex data distributions with different shapes and orientations. The Expectation-Maximization (EM) algorithm is used to learn the parameters of the GMM from the data. This approach provides a soft assignment, allowing for more nuanced insights into the data, which is particularly useful when there is uncertainty in the data points. However, GMM assumes that all data points are generated from a mixture of Gaussian distributions without considering outliers, which may be the reason for sub-optimal results. Similar to K-Means, GMM is sensitive to initialization and we ran GMM multiple times to ensure best results.
The supervised UMAP embeddings (described in the preproccesing section)for cancerous samples were used as inputs for the clustering algorithms. All algorithms utilize k=8 for the eight cancer types. The ground truth labels were used as external evaluation of the clustering methods.
Evaluation metrics
We chose the following two evaluation metrics because they provide insight into different aspects of clustering quality:
-
Adjusted Rand Index (ARI): measures the similarity between two clusterings by considering all pairs of samples and counting pairs that are assigned in the same or different clusters in both the true and predicted clusterings. It provides a score between -1 and 1, where 1 indicates perfect clustering agreement, 0 indicates clustering no better than random, and negative values indicate worse than random clustering.
-
Normalized Mutual Information (NMI): measures the mutual information between the true and predicted clusterings, normalized by the entropy of the true and predicted clusterings. It provides a value between 0 and 1, where 0 indicates no mutual information (clustering is random) and 1 indicates perfect agreement.
Classification
Using cfDNA data for cancer diagnosis consists of two steps: (i) cancer detection: determining whether a sample is healthy or cancerous, and (ii) cancer origin detection: determining the cancer type if the sample is cancerous. We created a sequential classification pipeline. The first binary classification model learns to classify Healthy vs Cancer using all training samples. The next set of binary classification models learns to classify Cancer A present vs absent, Cancer B present vs absent, etc., by training on only cancer samples. At inference time, the two sets of models are run sequentially. A patient’s sample is first determined whether healthy of cancerous. If predicted as healthy, the probability for all cancer types is assigned to 0. If predicted as cancerous, the binary cancer type classification models are run. Note that we are not using multi-class classification of cancer type because one sample could contain multiple types of cancer.
Models
We used two supervised machine learning models for classification:
Random forest is an ensemble learning method built upon the genral concept of bootstrap aggregating(bagging) and random feature selection. They are used for both classification and regression tasks. Random Forest operates by constructing a multitude of decision trees at training time and aggregating the predictions from each individual tree by voting. Random forests are robust to noise, easy to use and interpret, and are robust with respect to hyperparameter selection. They also do not require scaled data. The bagging and random feature selection at each split help to reduce the variance of the model and prevent overfitting without increasing the bias, which can be a problem in single decision tree models. Random Forests do not make any assumptions about the distribution of data, and are therefore particularly useful when working with non-linear datasets. They can be computationally more expensive to train depending on the number of trees and depth of each tree. This may be a limiting factor for very large datasets. Given that our dataset was small, computational resources were not a big concern.
Logistic regression predicts the probability of given sample belonging to a certain class, which is transformed into a binary outcome via a decision threshold such as 0.5. The probabilities are modeled using a logistic function or the sigmoid function that outputs values between 0 and 1. The logistic function is defined as:
p(y = 1 \mid x) = \frac{1}{1 + e^{-x \theta}}
Here, xθ is the linear combination of features, where x represents the features of a given sample and θ values are estimated from maximum likelihood estimation (MLE) to find the best fit of the model given the data. If the probability of belonging to a certain class $P(y = 1 \mid x)$ is greater than or equal to a threshold (e.g., 0.5), the observation is predicted to be in the default class; otherwise, it is predicted to be in the other class (i.e., 0 in this case). Logistic regression assumes a linear relationship between the log-odds of the dependent and each independent variable and is easy to interpret because the coefficients directly represent the strength and direction of association of each feature with the log odds of the dependent variable. This linear assumption may limit its effectiveness with complex datasets, such as gene expression, where relationships may be non-linear. Therefore, cross validation is important for understanding the performance of logistic regression in our study. Logistic regression is computationally less intensive, making it a good choice for capturing approximately linear relationships when the problem size does not justify more complex methods.
These models are chosen because they have lower overfitting risk, which is important for our small dataset, and good interpretability in terms of computing top contributing features.
Evaluation metrics
Receiver operating characteristic curve (ROC) and area under the ROC curve (AUC) are important evaluation metrics for calculating the performance of classification models. The ROC plots the true positive rate (also known as sensitivity or recall) and the false positive rate at different thresholds. When the threshold is lowered, both true and false positives increase. The ROC curve helps in visualizing this trade-off between benefiting from true positives and suffering from false positives. AUC plots model performance across all potential classification thresholds and provides the area under the ROC curve from (0,0) to (1,1) as a single number that can be compared between models. AUC represents the likelihood that a randomly chosen positive example is ranked more highly than a randomly chosen negative example. A higher AUC indicates a better performing model. An AUC = 0.5 represents a model with no discrimination capacity, essentially random guessing. An AUC = 1 represents a perfect model that perfectly discriminates positive from negative classes. An AUC of 0.7 to 0.8 is generally considered acceptable and an AUC of 0.8 to 0.9 is considered excellent for most practical purposes. For medical diagnostics, a model with a high AUC is preferred as it ensures that patients with a disease are correctly identified with fewer false alarms. However, the choice of threshold to convert probability scores into class predictions depends on the relative costs of false positives versus false negatives. For example, in cancer screening, missing a diagnosis (false negative) can be more dangerous than a false alarm (false positive), so a threshold that maximizes true positives (even at the expense of increasing false positives) might be chosen.
Hyperparameter Tuning
The number of components to include after dimension reduction is a hyper-parameter for each model, meaning we needed to use cross validation (CV) to determine the optimal count. For each model, we evaluated classification performance over a range of PLS component counts (from 2 to 20 for cancer detection and 2 to 15 for cancer origin classification). Note that we caped the maximum number of components to be smaller for the cancer origin classification models because the training sample size is smaller for these tasks. For each model, the component count with the highest CV AUC was selected. Figure 3 shows an example for choosing the number of PLS components for the cancer detection model.
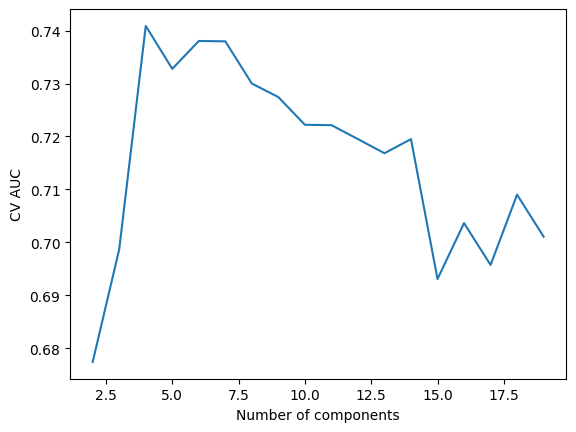
Figure 4: Choosing the number of PLS components for the healthy vs. cancer model.
Gene Contributions
In addition to predicting cancer classifications, supervised learning can be helpful for understanding which features are most strongly associated with classification. Although this does not indicate causation, determining genes that are strongly associated with outcomes creates a list of genes that may be potential therapeutic targets. Because our input features for random forests and logistic regression were the PLS components, we needed to multiply the importance weights (random forest classifier) or coefficients (logistic regression) by the gene loadings of the PLS components used in the models. To do this, we used matrix multiplication between a 1xC matrix of PLS component importances/coefficients and a CxD matrix of gene loadings (mapping C PLS components back to D genes) to get a 1xD matrix of gene contributions for each classification.
Strategies to Address Data Imbalance
One major limitation of our study design is the small number of positive samples for each cancer type relative to the whole dataset. We addressed these issues with data augmentation and class-weighted cost functions.
Data Augmentation with SMOTE
We used Synthetic Minority Over-sampling Technique (SMOTE; [2] ) to test if augmenting our data with additional simulated positive samples for each cancer type would improve our model accuracy and AUC. SMOTE is a popular method to address the issue of class imbalance in machine learning datasets, particularly when the minority class has significantly fewer examples than the majority class. In imbalanced classification, the minority class has too few examples for the model to effectively learn the decision boundary. This imbalance can skew the model’s performance, often favoring the majority class. The simplest form of addressing this imbalance is by oversampling the minority class through duplication of its examples. While this balances the class distribution, it does not introduce any new information to the model, potentially hindering its ability to generalize. SMOTE goes a step further by synthesizing new minority examples rather than merely duplicating existing ones. This method involves the following steps:
- Selection of Sample: Randomly pick an instance of the minority class.
- Neighbor Calculation: Identify k-nearest neighbors of this instance, typically using k=5.
- Synthesis of New Samples: Select one of these neighbors and generate new samples along the line that connects the chosen instance and its neighbor in the feature space. The new sample is a convex combination of the two points, essentially creating a “synthetic” example.
Benefits of SMOTE include:
- Balanced Classes: It helps balance the class distribution without losing valuable information, unlike simple duplication.
- Enhances Learning: By generating new, plausible examples, SMOTE allows the model to learn more generalizable decision boundaries.
Limitations
- SMOTE does not consider the position of the majority class examples while generating synthetic samples, which can lead to the creation of ambiguous samples especially in regions where the classes overlap.
- Feature Space Dependence: The effectiveness of SMOTE depends on the assumption that the minority class instances are not isolated; rather, they form a dense area in the feature space.
SMOTE is often used in conjunction with under-sampling of the majority class. This combination is found to be more effective than using under-sampling or SMOTE alone, as it enriches the dataset with more diverse examples from the minority class while reducing the size of the majority class.
Class-weighted cost functions
Instead of synthesizing data points to address class imbalance, the class-weighted cost function over or under samples the classes that are under or overrepresented, respectively. To do this, we implemented both the random forest classifier and the logistic regression classifier with the class_weight=”balanced” option in scikit-learn. This mode automatically adjusts weights inversely proportional to class frequencies in the input data as
n_{samples} / (n_{classes} * numpy.bincount(y))
Benefits of class-weight cost functions include:
- Improved Model Fairness: By weighting the loss function, the model is more likely to treat each class fairly, even if some classes are underrepresented. This prevents the model from being biased toward the majority class.
- Better Performance on Minority Classes: Increasing the weight of the minority classes in the loss function makes the model pay more attention to these classes, often leading to better accuracy and recall for these groups.
- Flexible Adjustments: Weights can be adjusted according to specific needs or based on the importance of certain classes, offering flexibility in tuning the model’s sensitivity toward different classes.
- Compatibility with Existing Models: Class weighting can be integrated into virtually any model that uses a loss function, making it a versatile solution that can be applied without altering the underlying architecture of the model.
Limitations
- Potential for Overfitting: Heavily weighting the minority class can cause the model to overfit to these classes, particularly if they contain noisy or non-representative data, leading to poor generalization on unseen data.
- Dependence on Sufficient Data: If the minority class has very few examples, simply adjusting the weights might not be enough to learn meaningful genralizable patterns. In such cases, other techniques like SMOTE might be necessary, potentially in conjunction with weighting.
References
- B. Muzellec, M. Telenczuk, V. Cabeli, and M. Andreux, “PyDESeq2: a python package for bulk RNA-seq differential expression analysis,” Bioinformatics, 2023, doi: 10.1093/bioinformatics/btad547.
- N. V. Chawla, K. W. Bowyer, L. O. Hall, and W. P. Kegelmeyer, “SMOTE: synthetic minority over-sampling technique,” Journal of artificial intelligence research, vol. 16, pp. 321–357, 2002.